Polar Star Quantitative Commodity Fund
Dr Mauritz van den Worm, PhD
17 February, 2021
Overview
- Portfolio manager background
- Cyclic nature of commodity markets
- Long term drivers of commodity prices
- Philosophy of taking many small bets
- The core strategies
- Portfolio
Portfolio Manager Background
Education
PhD in Quantum Physics from Stellenbosch University - 2015
Applications:
- Rapid information transfer in quantum systems
- Spreading of correlations in quantum systems
- Theory of trapped ion quantum simulators
- Wishlist: Development of quantum computers
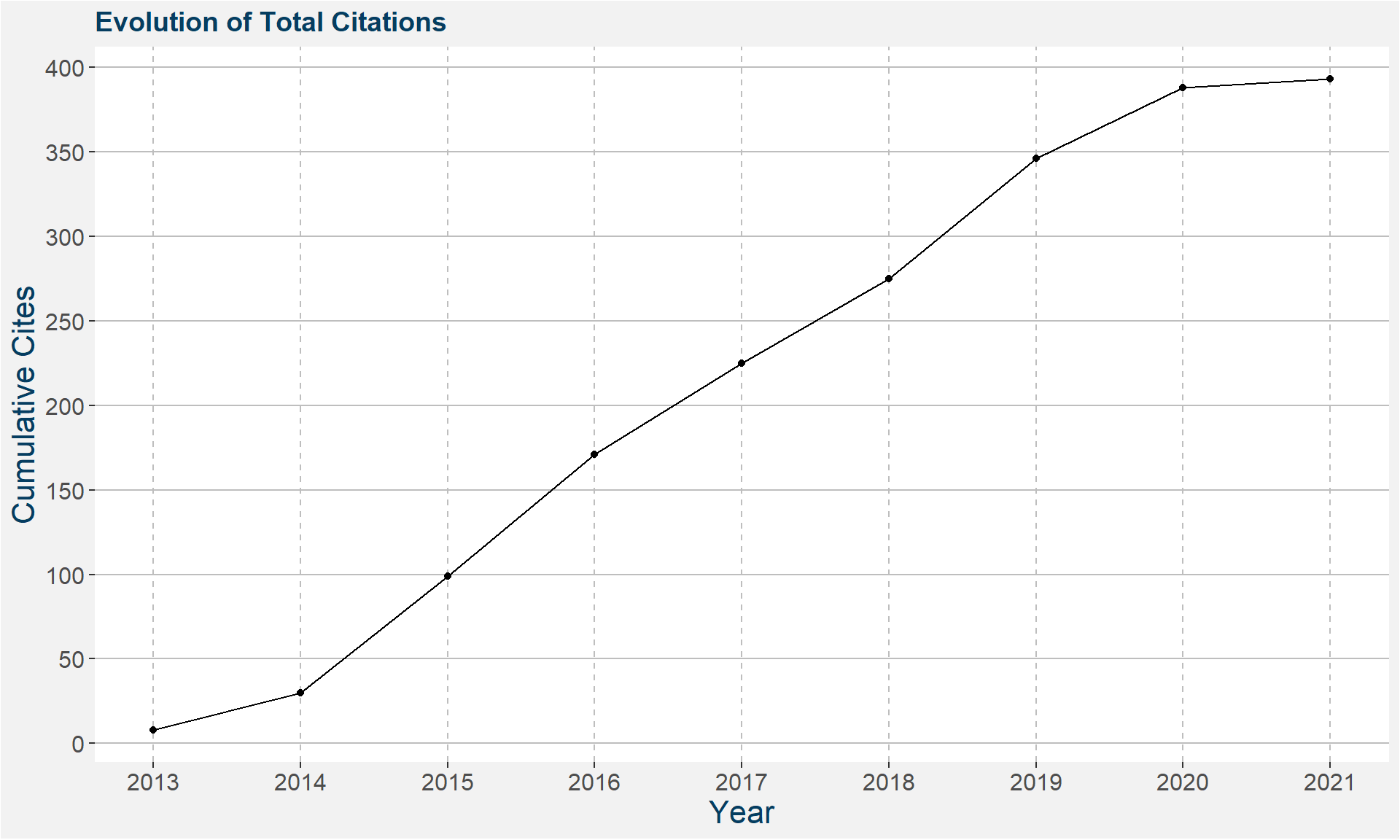
Most Cited Peer Reviewed Fundamental Research
- Breakdown of Quasilocality in Long-Range Quantum Lattice Models
- J Eisert, M van den Worm, SR Manmana and M Kastner
- Physical Review Letters 111 (26), 260401
- Cited by 144
- Relaxation timescales and decay of correlations in a long-range interacting quantum simulator
- M van den Worm, BC Sawyer, JJ Bollinger and M Mastner
- New Journal of Physics 15, 083007
- Cited by 105
- Quantum correlations and entanglement in far-from-equilibrium spin systems
- KRA Hazzard, Mvan den Worm, et al.
- Physical Review A 90 (6), 063622
- Cited by 94
Citation History
Coauthor Network

Time at Polar Star

Cyclic Nature of Commodity Markets
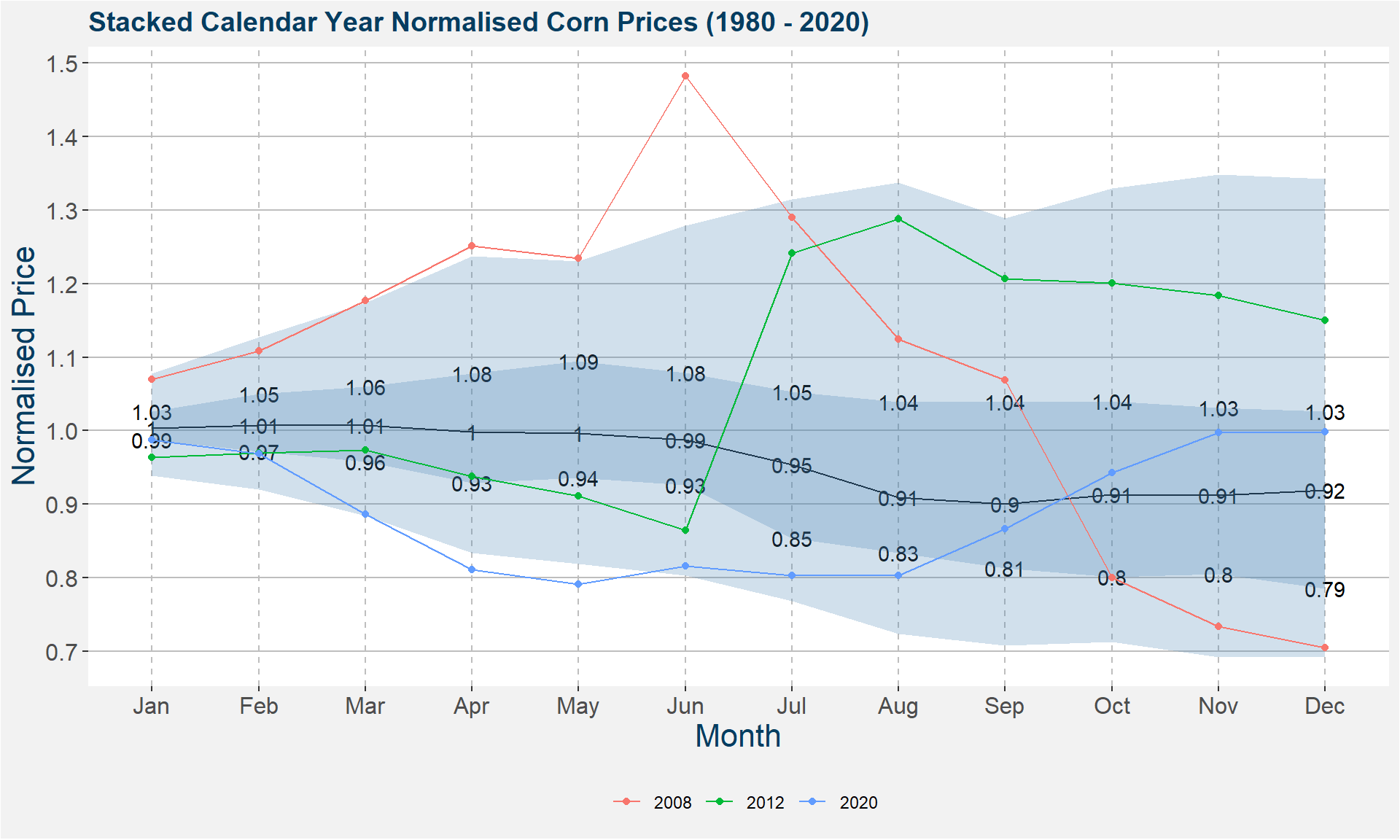
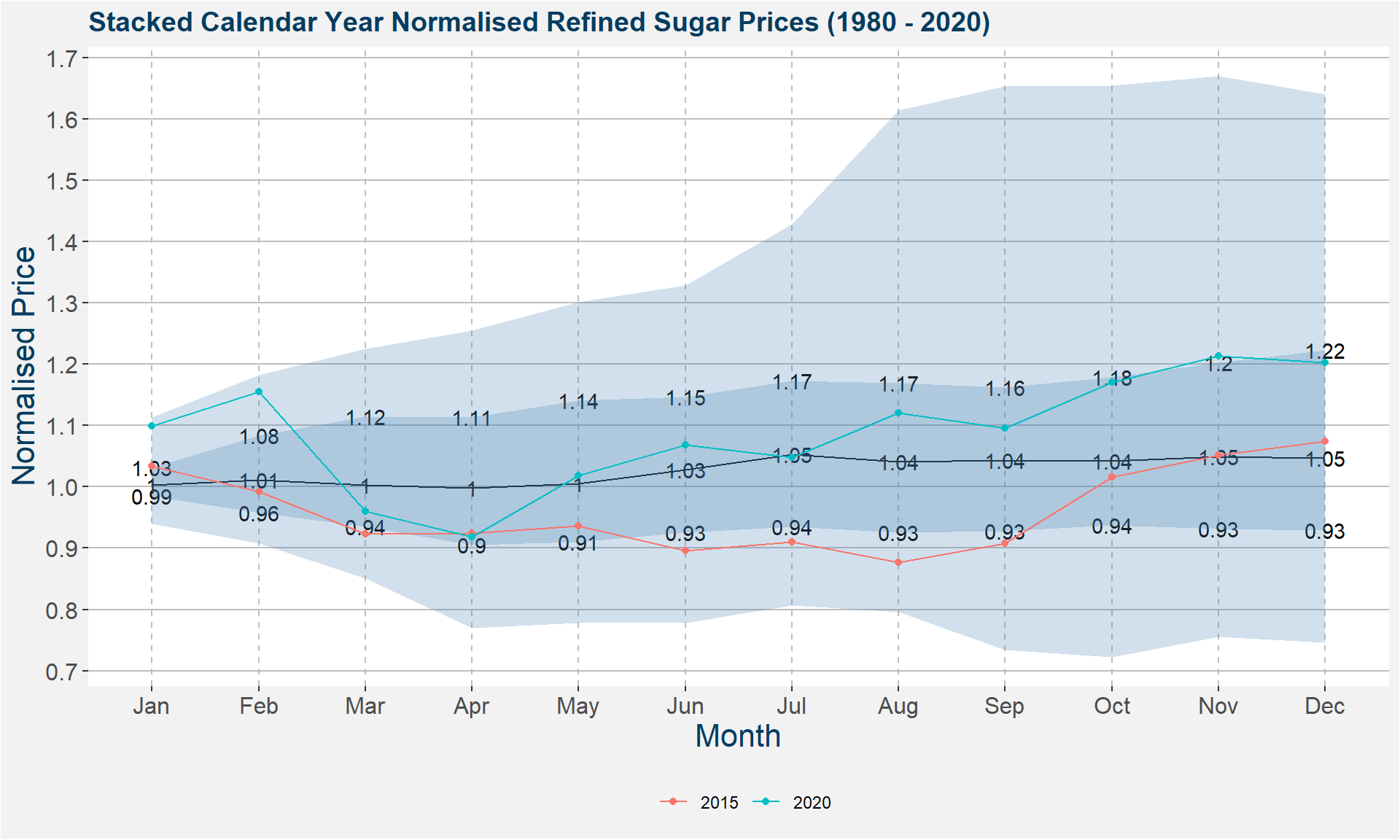
Corn Life Cycle

Corn Calendar Spread Example

Lean Hog Calendar Spread Example
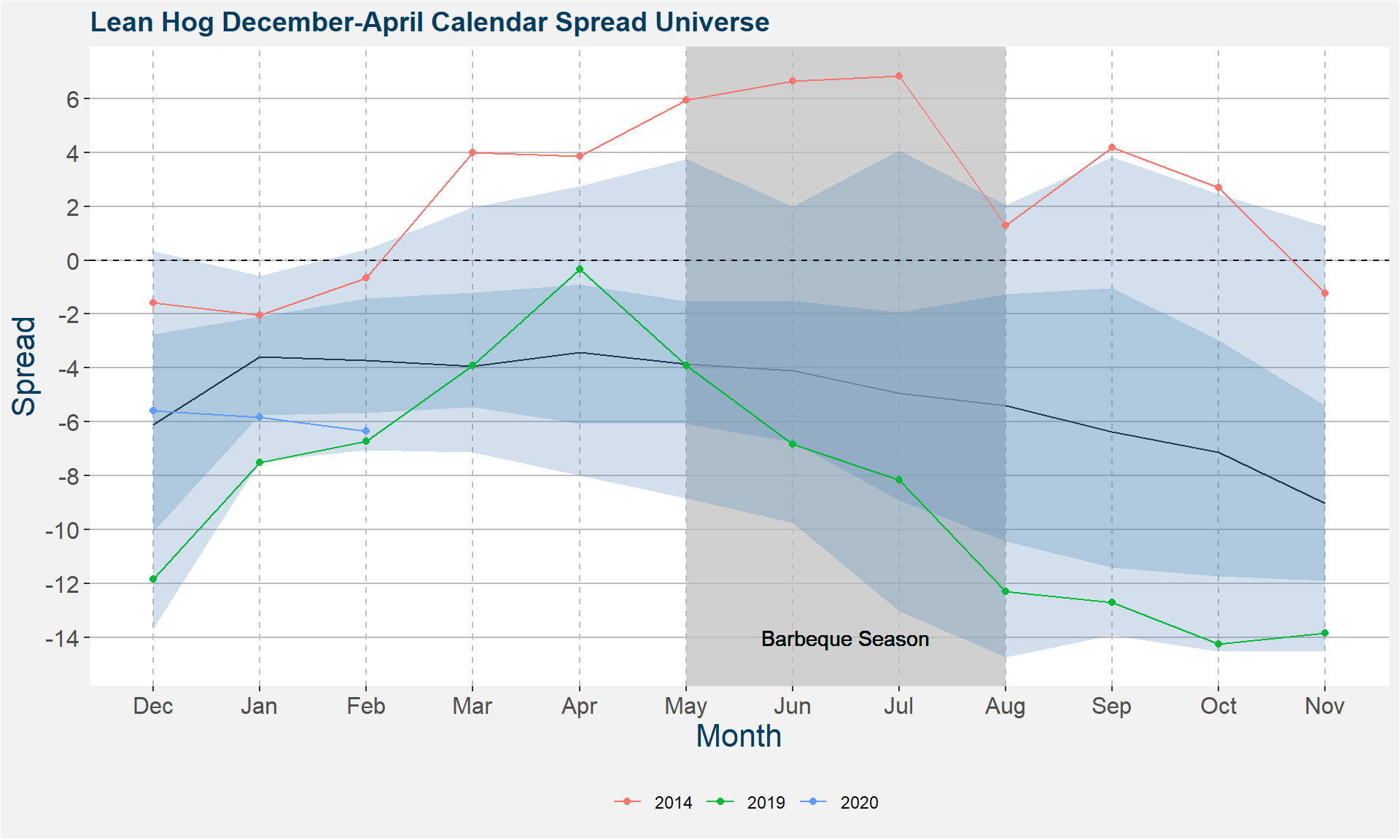
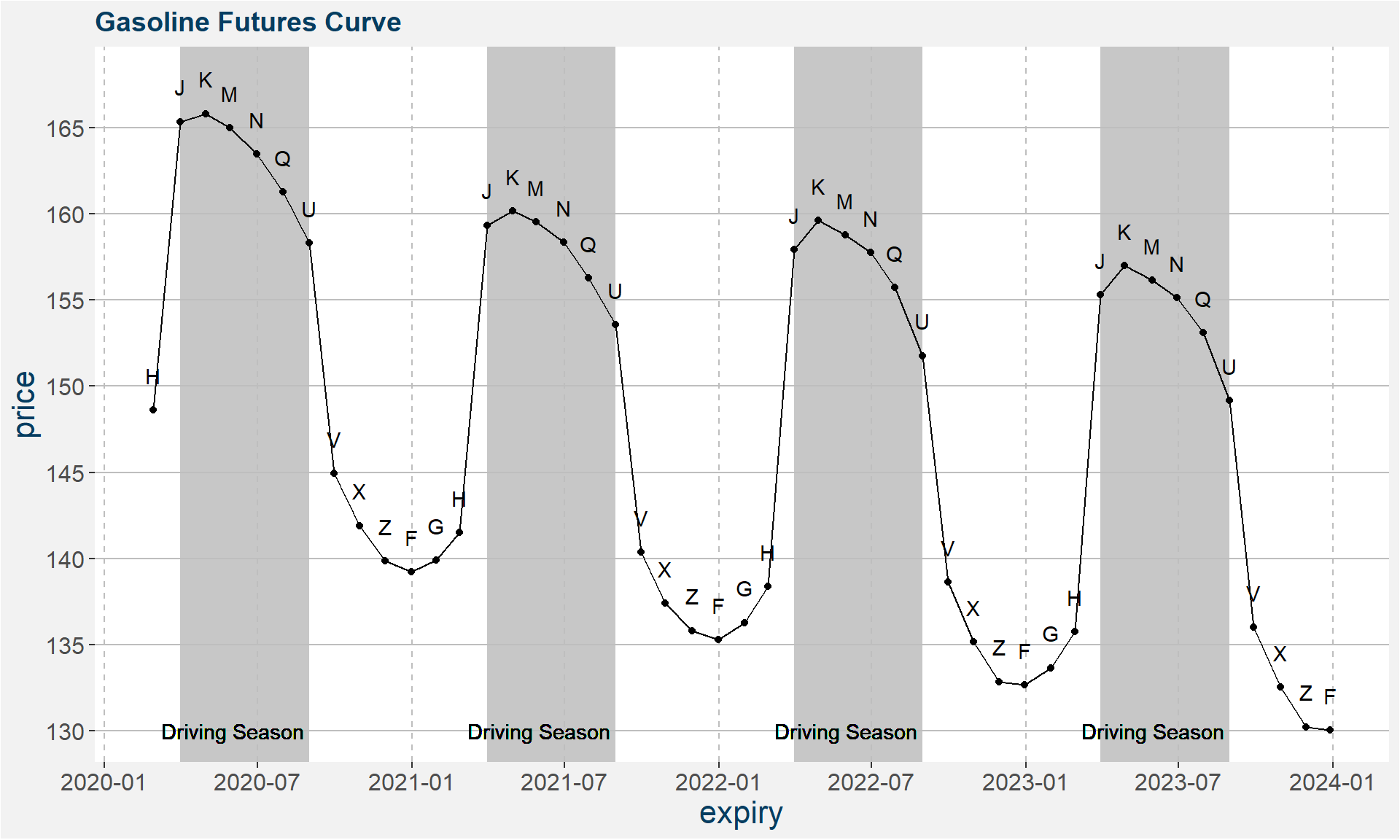
RBOB Gasoline Curve Example
Long Term Drivers of Commodity Markets
Curve Structure - Contango

Curve Structure - Backwardation
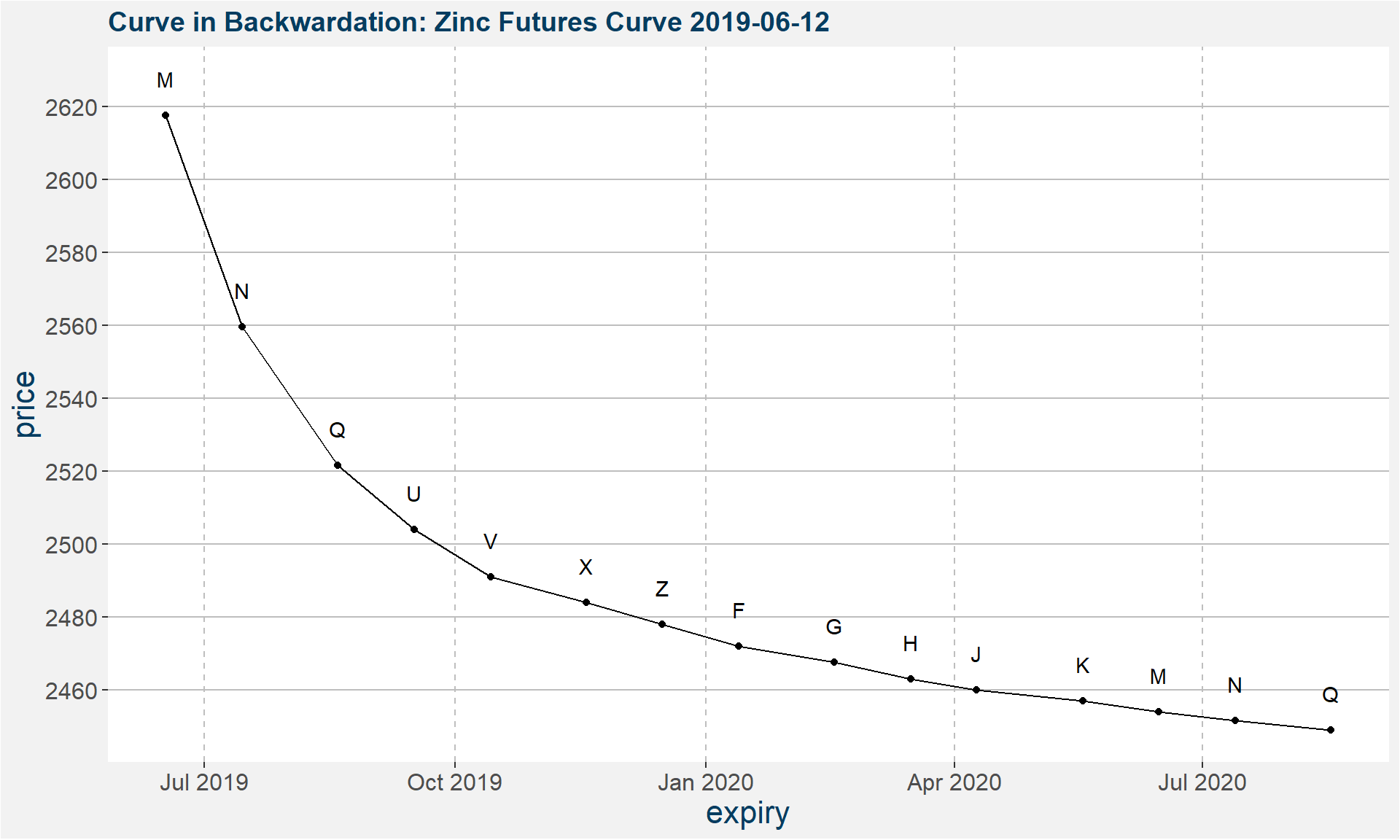
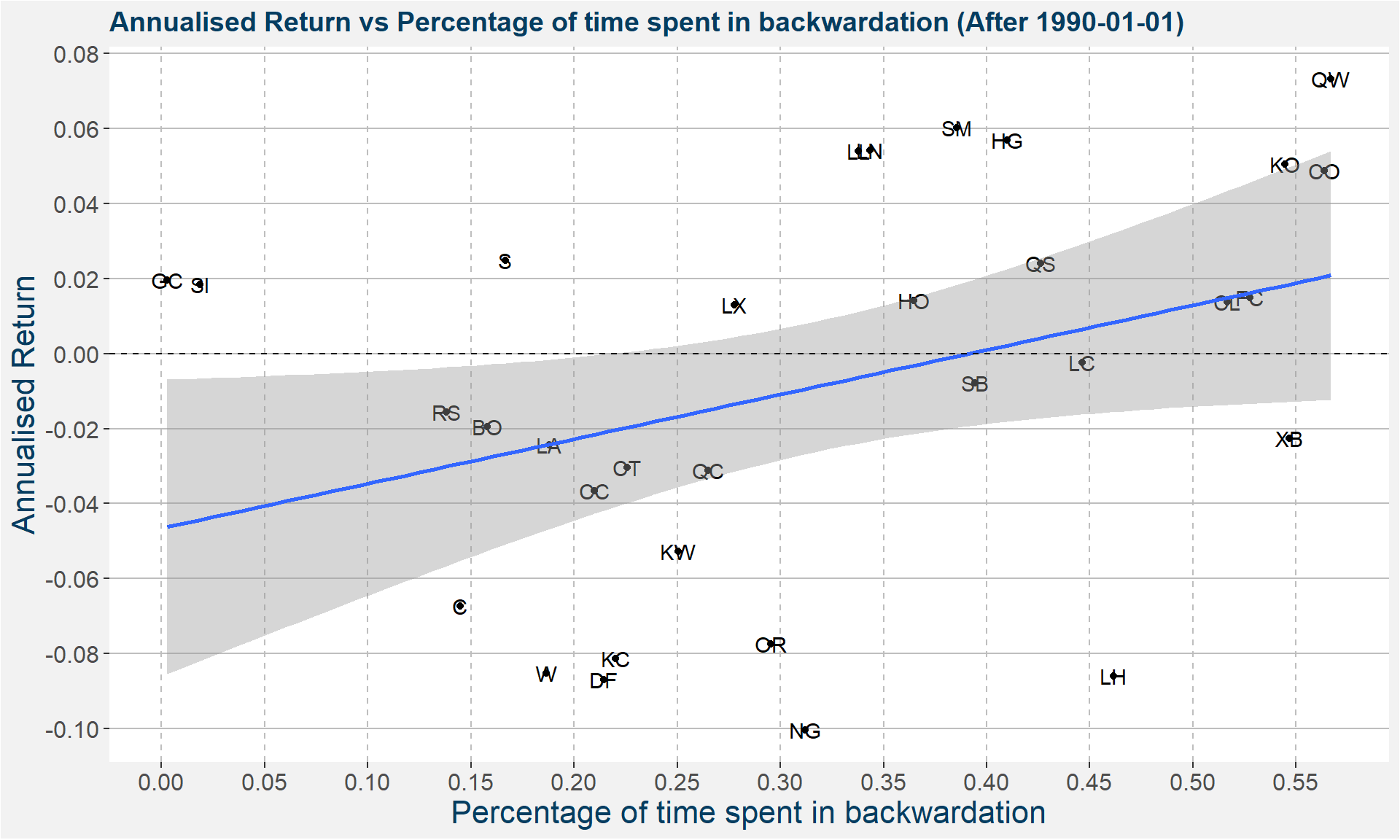
How the Curve Structure Affects Prices (1/4)

How the Curve Structure Affects Prices (2/4)
How the Curve Structure Affects Prices (3/4)

How the Curve Structure Affects Prices (4/4)
Backwardation and Annualised Return
Using the Curve in your favour
- Each commodity has a different curve structure
- You can think of the curve structure as a tide
- It is much easier to swim with the tide than against it
- For many commodities the curve structure has cyclical behaviour
- Using Curve Carry we try to exploit this
- Using the curve structure in a trend strategy helps in entering profitable long term trades
Philosophy of Taking Many Small Bets
Fundamental Law of Portfolio Management
\[ \large \text{Performance} = \text{Skill} \times \sqrt{\text{Breadth}} \]
- Skill measures your ability to find profitable opportunities
- Breadth captures how many opportunities you have available
Coin Flipping Casino (1/5)
- We know the coin is biased with \(P(\text{heads}) = 0.51\)
- We have 1000 coins
- The minimum wager is 1 coin
- If you win you gain 1 coin
- If you loose you loose 1 coin
- There are 1000 tables with coin wagers
Coin Flipping Casino (2/5)
How do we place the bets?
Two extremes:
- Bet 1000 coins on one coin flip
- Bet 1 coin on 1000 coin flips
Coin Flipping Casino (3/5)
The same expected return:
- Single bet: \(0.51 \times 1000 + 0.49 \times (-1000) = 20\)
- Multi bet: \(1000 \times [0.51 + 0.49 \times (-1)] = 20\)
Totally different risk to loose it all:
- Single bet: 49%
- Multi bet: \(0.49 \times 0.49 \times \dots \times 0.49 = 0.49^{1000} \approx 0\)
Coin Flipping Casino (4/5)
Another way to look at risk is to use standard deviation of returns
- Multi bet:
\[ \text{risk} := \text{std}\left\{1,-1,-1,1, \dots, 1 \right\} = 1 \]
- Single bet:
\[ \begin{align} \text{risk} &:= \text{std}\left\{1000,0,0,0, \dots, 0 \right\} = 31.62 \\ \text{risk} &:= \text{std}\left\{-1000,0,0,0, \dots, 0 \right\} = 31.62 \end{align} \]
Coin Flipping Casino (5/5)
Risk Adjusted Returns (Sharpe Ratio):
- Single bet: \(\text{SR}_{\text{single}} = \frac{20}{31.62} =0.63\)
- Multi bet: \(\text{SR}_{\text{multiple}} = \frac{20}{1} =20\)
We rewrite the risk adjusted return as:
- \(20 = 0.63 \times \sqrt{1000}\)
- \(\text{SR}_{\text{multiple}} = \text{SR}_{\text{single}} \times \sqrt{\text{Bets}}\)
- \(\text{Performance} = \text{Skill} \times \sqrt{\text{Breadth}}\)
Three Pillars of Diversification
- What you trade
- Different commodities
- Different calendar spreads
- Different parts of the curve
- How you trade
- Trend
- Curve Carry
- When you trade
- Different signals
- Different times of the year
- Roll methodology and timing
All of these add to the breadth of opportunities.
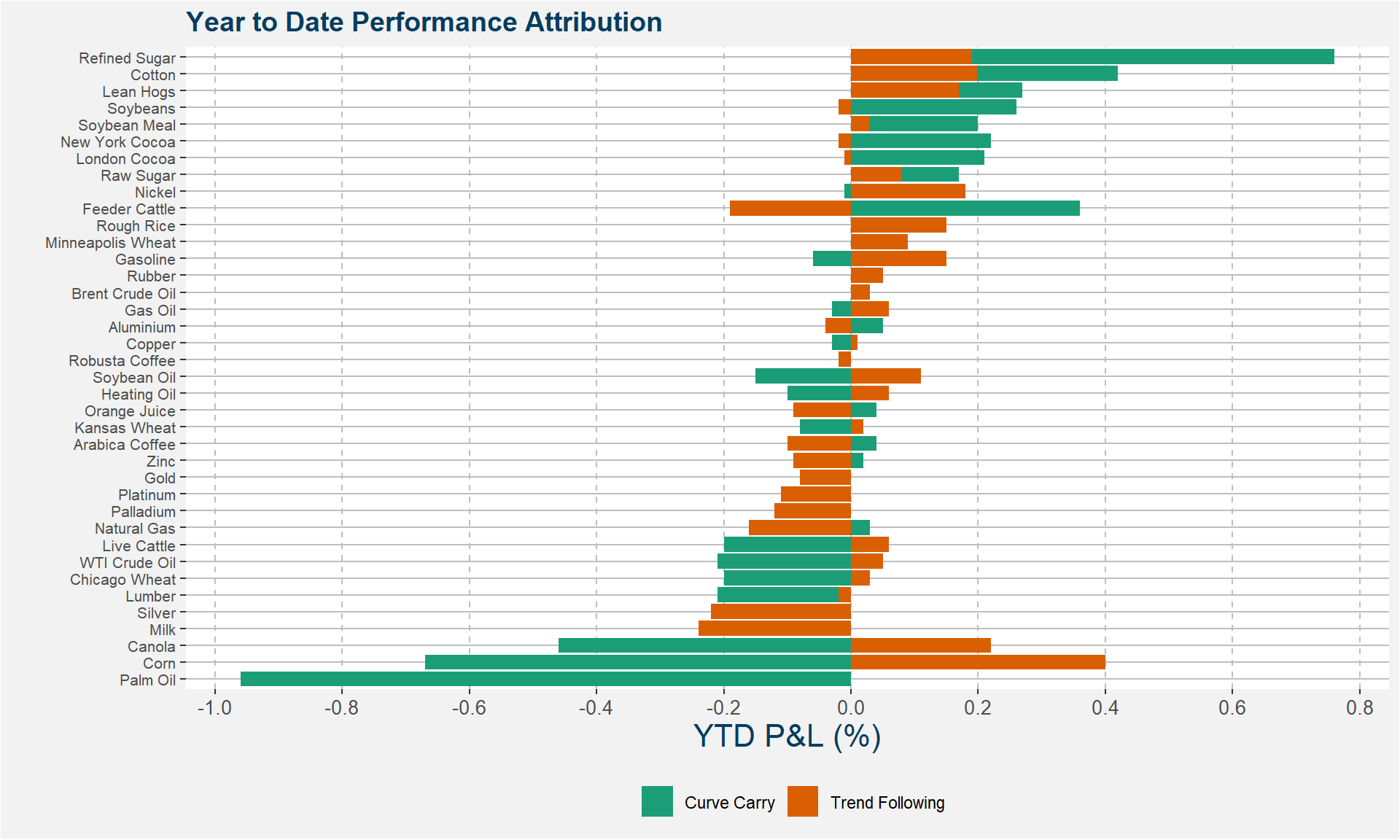
View of Current Book
Core Strategies
- Curve Carry
- Trend Following
Testing phase:
- Relative Roll
- Deferred Carry
- Relative Calendars
Curve Carry (1/n)
Aim of the strategy:
- Harness the curve carry
- Storable commodities have predictable cuve structure
- Higher stock levels are associated with contango curves
- Many commodities evolve into a contango as the front nears expiry
We define \(p\) as the ratio of the Front to the Deferred price \[ p := \text{Front}/\text{Deferred} \]
- When \(p\) < 1 the Front is trading at a discount to the Deferred.
- The smaller \(p\) the greater the contango
Curve Carry (2/n)

Curve Carry (3/n)

Curve Carry (4/n)
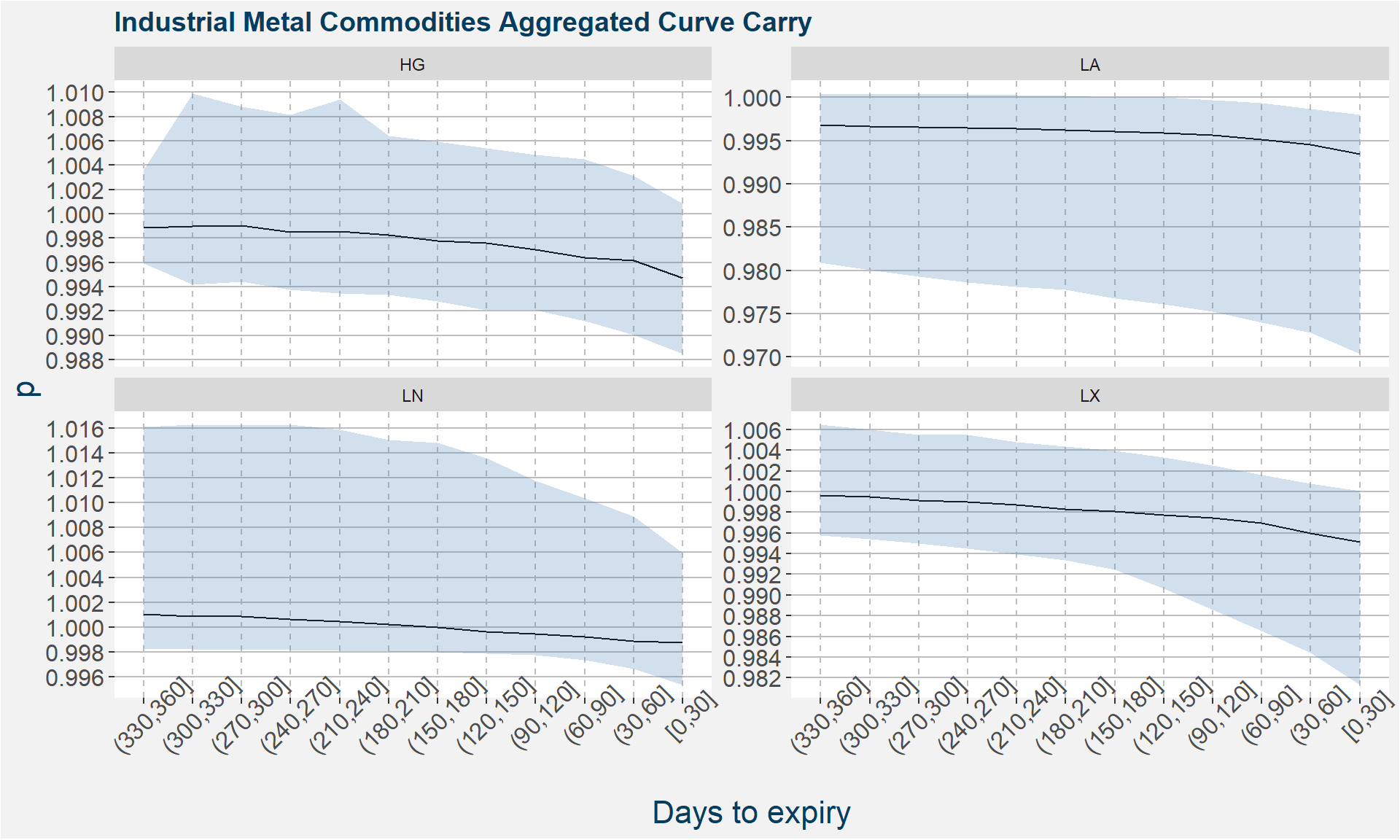
Curve Carry (5/n)

Curve Carry (6/n)
From a fundamental point of view we
- Identify commodity calendar spread pairs
- With predictable behaviour during certain parts of the year
For every month of the year we have a list of
- Commodities,
- Associated calendar spread we want to be involved with and
- The side of the trade
Meta-labeling: ML Technique to determine probability of the spread ending in the money
Size positions according to the
- Volatility and
- Probability of profit
- Lower volatility receives a higher allocation
Curve Carry (7/n)
Curve Carry - Risk and Return Statistics (8/n)
Curve Carry - Time Windown Report (9/n)
Time Window Analysis:
Drawdown Report:
Trend Following (1/n)
Aim of the strategy:
- Trade commodity trends profitably
- Lookback windows ranging from a couple of weeks to one year
- Collection of signals:
- Breakout,
- Donchain and
- Exponential Moving average signals
- Target volatility 20%
- Diverse universe of commodities
- Multiple parts of the futures curves
- Roll structure created from fundamental understanding
Essence: Cap your losses and let the winners run
Trend Following (2/n)
Build the strategy on fake data:
- Create data with trends
- See if we can trade it profitably
- Investigate price behaviour that cannot be traded profitably
Why is this preferred:
- No overfitting of the underlying market data
- Datamined lookbacks and models perform great in sample
- Majestic performance is difficult to follow up on new data
Trend Following (3/n)
Trend Following (4/n)

Trend Following (5/n)
Trend Following - Risk and Return Statistics (6/n)
Trend Following - Time Windown Report (7/n)
Time Window Analysis:
Drawdown Report:
Trend Following - Recent Years (8/n)
You Can’t Always Trend When You Want - AQR
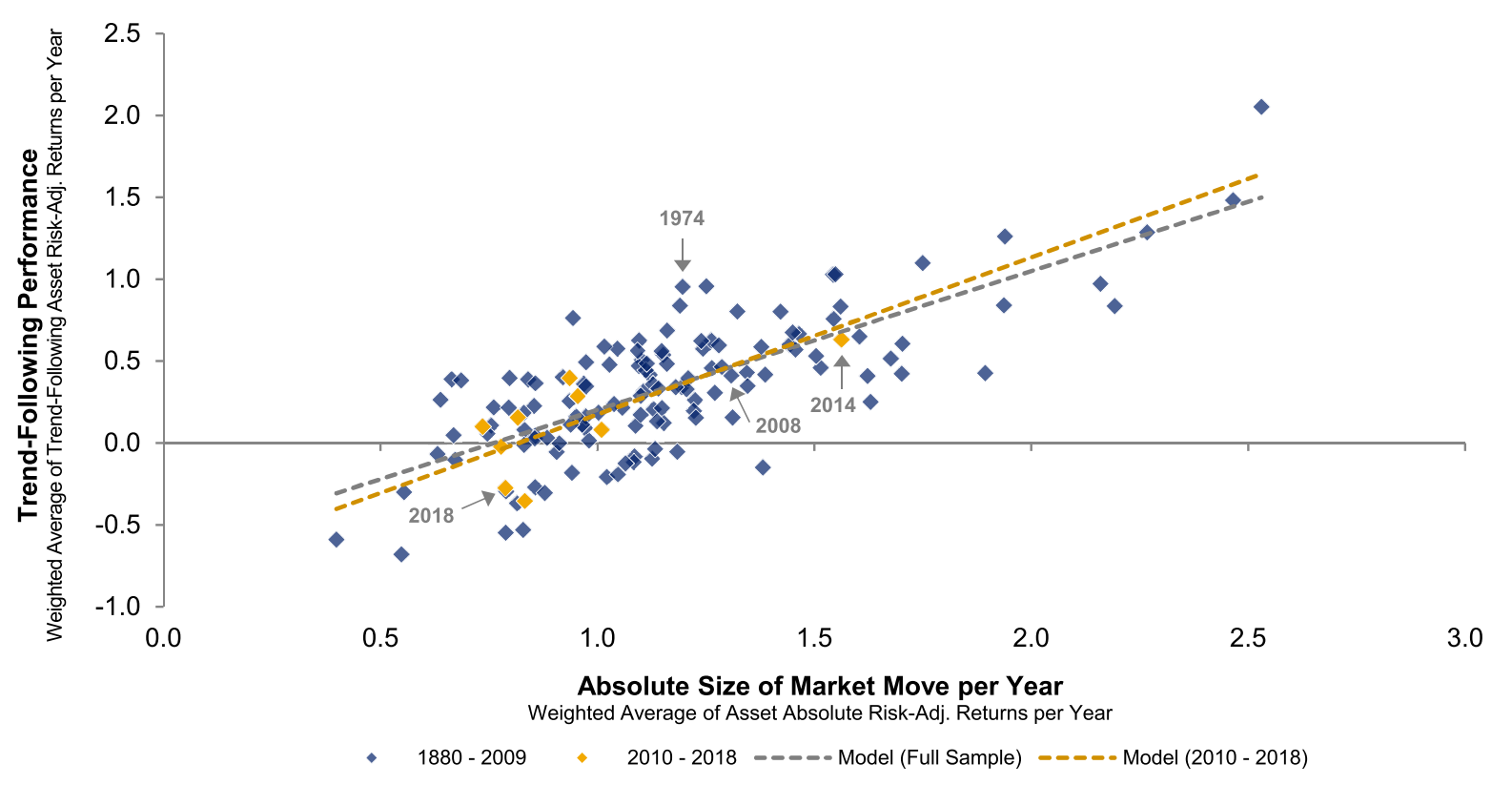
Trend Following - Recent Years (9/n)
Breaking Bad Trends - Garg, Goulding, Harvey and Mazzoleni
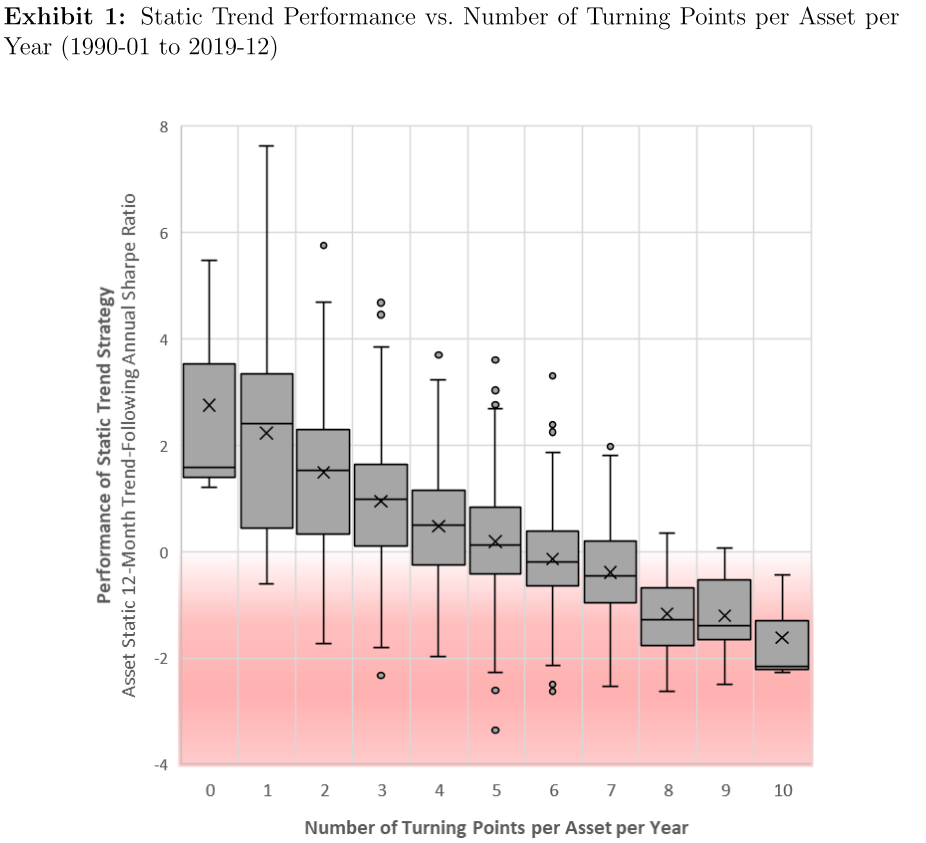
Trend Following - Recent Years (10/n)
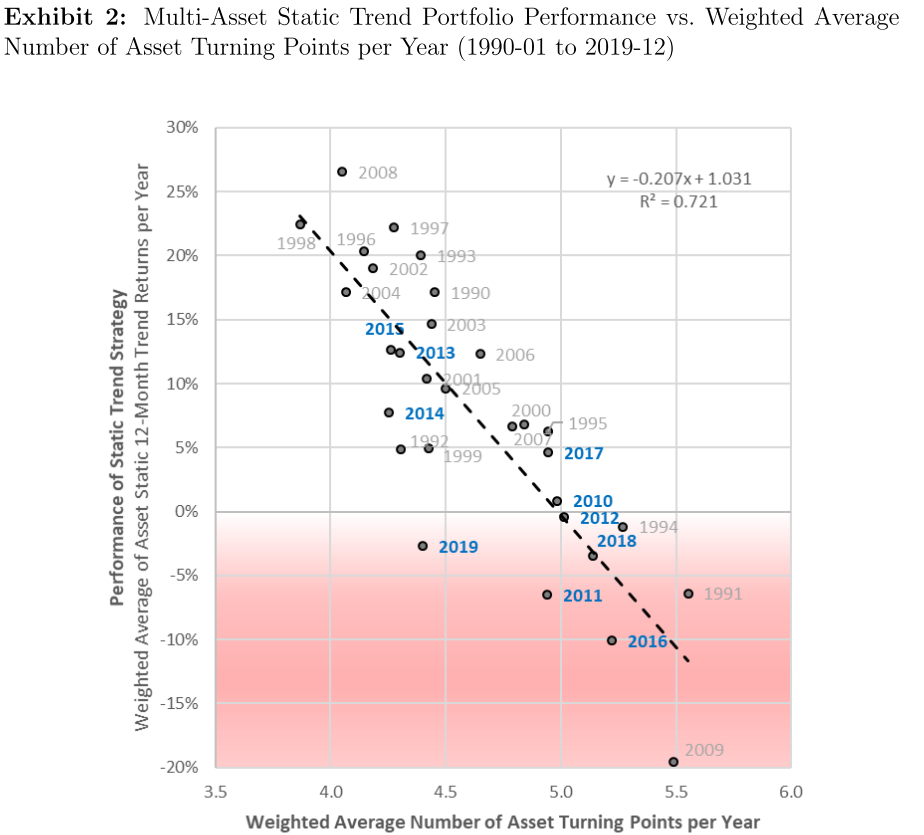
Why Curve Carry and Trend Following?
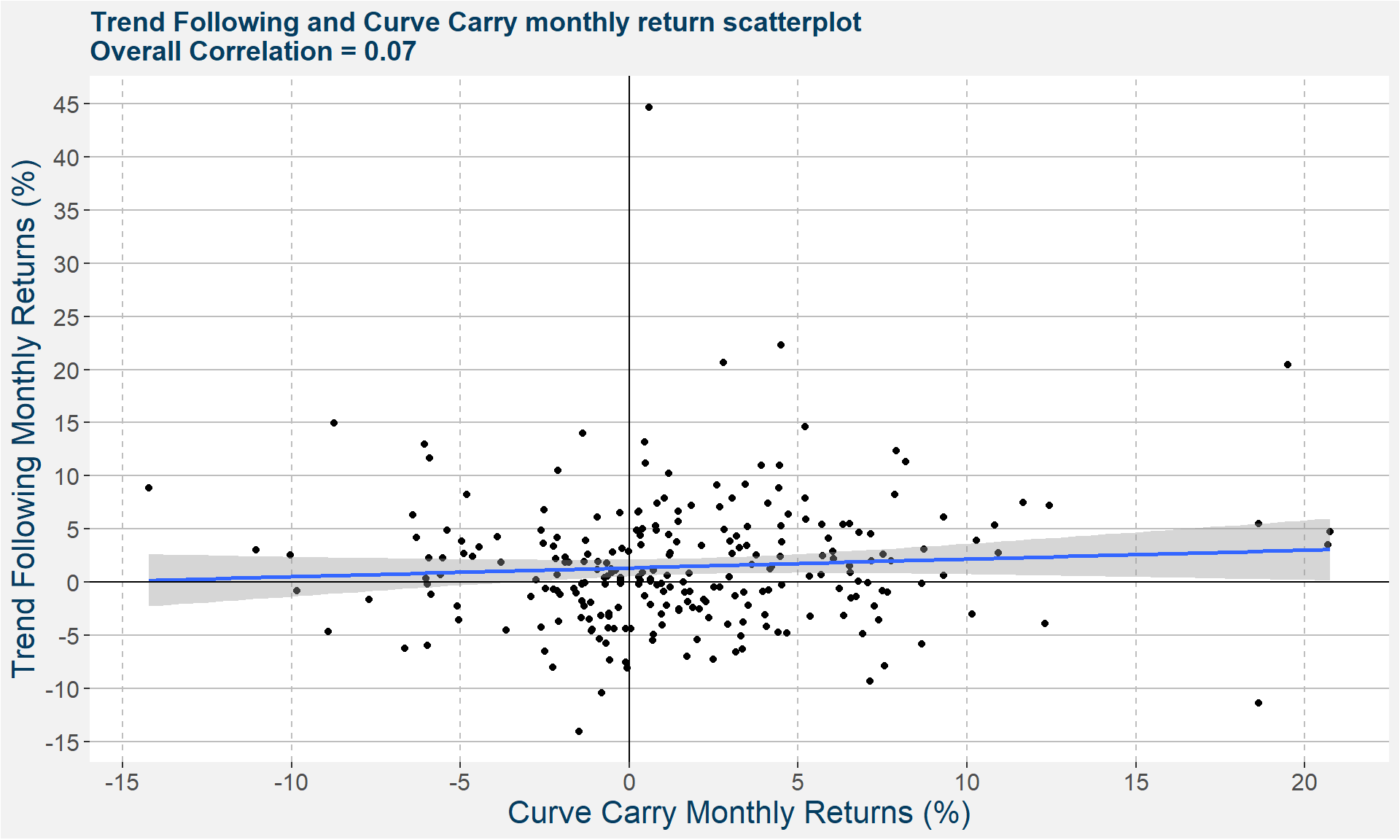
Return Scatterplot
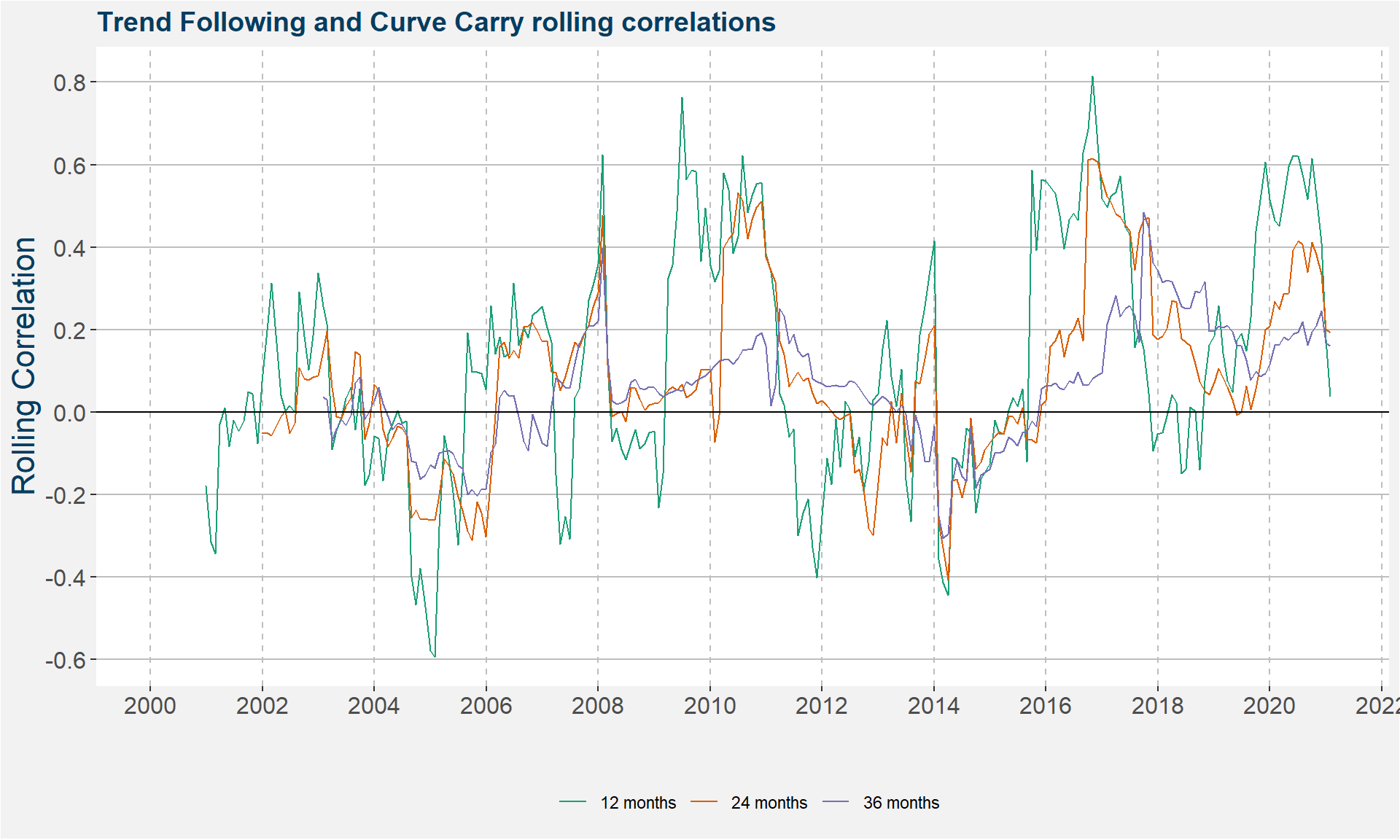
Rolling Correlations
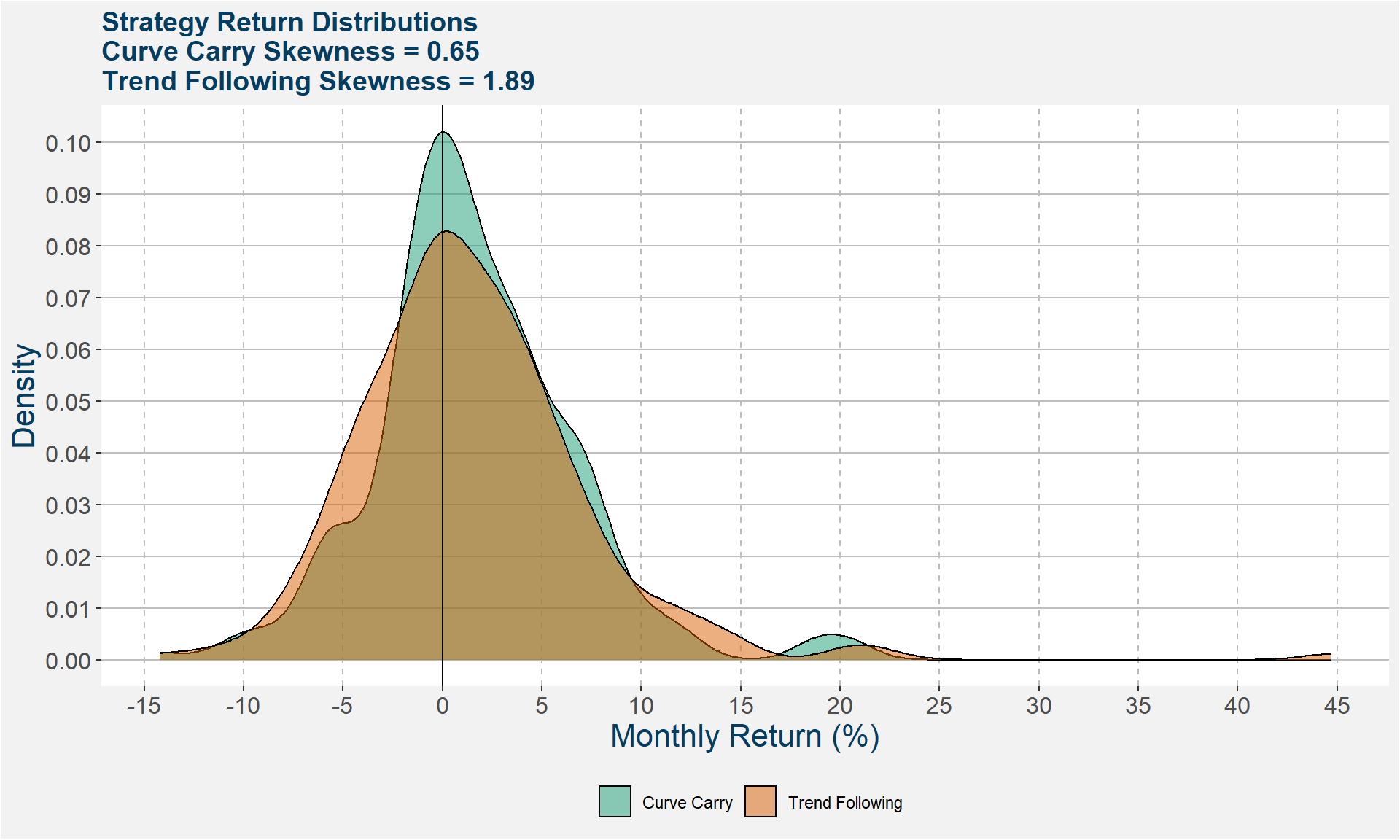
Return Distributions
Zig and Zag
Academic References
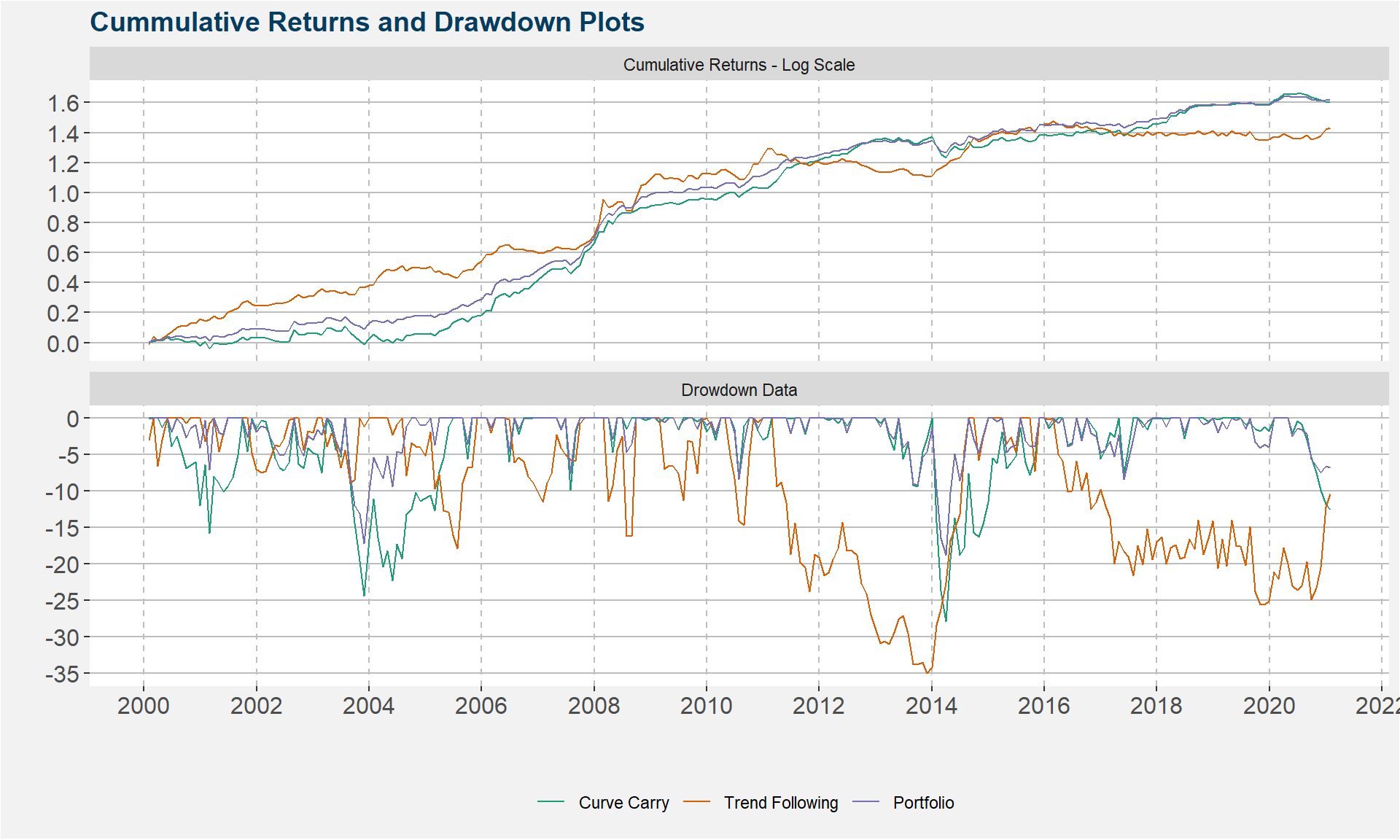
Portfolio
Portfolio View
Portfolio View - Risk and Return Statistics
Portfolio View - Time Windown Report
Time Window Analysis:
Drawdown Report:
Summary
What we hope to achieve
- Long term positive returns
- Exploit fundamental knowledge and curve structure
- Diversified quantitative commodity product
- Low correlation to
- other Polar Star funds,
- equities and
- commodity indices
